Rumus Bangun Ruang

Bangun ruang adalah suatu bangun yang memiliki sisi tiga dimensi seperti panjang, lebar dan tinggi (z, x, y). Jadi, selain memiliki luas, bangun ruang juga memiliki volume. Ini adalah perbedaan utama dari bangun datar yang hanya memiliki luas karena hanya berupa dua dimensi. Ada beberapa karakteristik khusus bangun ruang seperti :

1.Berupa bangun 3 dimensi
2.Memiliki volume
3.Memiliki panjang, lebar, tinggi (bola tetap disebut jari-jari)
4.Dapat dibuat jaring-jaringnya.

Berdasarkan karakteristik tersebut, ada banyak aneka bangun ruang yang sering kita jumpai. Berikut adalah beberapa contoh bangun ruang beserta rumus dan karakteristiknya masing-masing:

1. Rumus Volume KUBUS

Karakteristik Bangun Kubus sangat mudah untuk diingat, yakni :

1.Kubus memiliki 6 (enam) limas segitempat yang ada di dalamnya.
2.Kubus memiliki 6 (enam) buah sisi yang berbentuk persegi yang masing-masing luasnya sama
3.Kubus memiliki 12 (dua belas) rusuk yang semua panjangnya yang sama
4.Semua sudut kubus bernilai 90 derajat atau siku-siku
5.Rumus Volume Kubus = rusuk x rusuk x rusuk (rusuk pangkat 3)

V = r ³

• Rumus Keliling Kubus = 12 x rusuk

Kell = 12 r

• Rumus Luas Permukaan Kubus = 6 x rusuk x rusuk

L = 6 r²

• Luas salah satu sisi = rusuk x rusuk

L sisi = r²

2. Rumus Volume BALOK

Karakteristik Balok pada dasarnya mirip dengan kubus, hanya saja balok tidak memiliki panjang rusuk yang semuanya sama, atau panjang sisinya berbeda-beda. Karakteristik khusus balok, yakni:

• Rumus Volume Balok = pangjang x lebar x tinggi

V = p x l x t

• Luas Permukaan Balok = 2 x {(panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)}

L = 2 x {(pxl) + (pxt) + (lxt)}

• Keliling Balok = 4 x (panjang + lebar + tinggi)

Kell = 4 (p + l + t)

• Diagonal Ruang = Akar dari (panjang kuadrat + lebar kuadrat + tinggi kuadrat)

Diagonal Ruang = √(p² + l² + t ²)

3. Rumus Volume TABUNG

Tabung menyerupai balok, hanya saja, sisi tegaknya berupa lingkaran.

• Rumus Volume tabung = luas alas (lingkaran ) x tinggi tabung

V = π r ² t

• Rumus luas tabung /silinder = luas alas + luas tutup + luas selimut (karena luas alas dan tutup sama, jadi bisa juga ditulis = 2 luas alas + luas selimut)

L = 2 π r ² + 2 π r t

• Rumus luas selimut tabung

L selimut = 2 π r t

4. Rumus Volume KERUCUT

Kerucut berbentuk seperti caping. Bentuk kerucut dapat berasal dari tabung, hanya saja salah tidak memiliki tutup, melainkan menggunakan titik puncak tepat di tengah-tengah. Sebuah percobaan pernah menunjukkan tentang hubungan antara volume kerucut dan tabung.

Jika kamu memasukkan pasir penuh ke dalam sebuah kerucut, maka dengan volume/ jumlah pasir yang sama volumenya akan dapat memenuhi sebuah tabung dengan diameter dan tinggi yang sama dengan kerucut, tepat sebanyak tiga kali. Artinya, volume kerucut ini dapat kamu cari dengan menghitung sepertiga dari volume tabung (dengan diameter dan tinggi yang sama).

• Rumus Volume kerucut  = 1/3 x luas alas (lingkaran ) x tinggi

V =  ⅓ π r ² t

• Luas Kerucut = luas alas + luas selimut

L = π r ² + π r s

• Luas Selimut Kerucut

L = π r s

Simak juga: Gerak Lurus Beraturan (GLB)

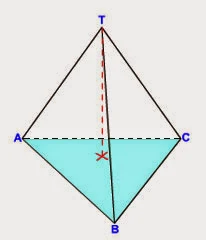
5. Rumus Volume LIMAS

Limas memiliki bentuk dasar seperti kerucut. Hanya bedanya, jika kerucut memiliki alas berbentuk lingkaran, maka limas memiliki alas yang dapat berupa bangun datar lain, misalnya segiempat, segitiga, segilima, dan lainnya.

Nama limas juga menyesuaikan dengan bentuk alasnya. Misal limas dengan alas segiempat, disebut sebagai limas segiempat, sementara limas dengan alas bentuk segitiga, maka disebut dengan limas segitiga.

• Rumus Volume Limas  = ⅓ x luas alas x tinggi sisi

V =  ⅓ La  x t

• Luas Kerucut = luas alas + jumlah luas sisi tegak (jumlah semua luas sisi yang ada)

L = La + Lsisi 1 + Lsisi 2 + …

• Untuk Limas Segitiga ada rumus volume tersendiri yang bisa memudahkan untuk menghitung, yakni:
  

V =  1/6 La  x t x T

(t = tinggi sisi segitiga, T = tinggi limas)

6. BOLA

Bola merupakan salah satu bangun ruang yang unik. Bola memiliki jari-jari atau diameter yang melingkar atau sama di setiap sudutnya.

• Rumus Volume tabung

V = 4/3 π r ³

• Rumus Luas Permukaan Bola

L = 4 π r ²

Catatan :

π  = Phi = 3,14 atau 22/7

rumus bangun ruang