Kumpulan Soal Luas dan Keliling Gabungan Bangun Datar, Matematika SD Kelas 6
Dalam matematika, bangun datar dapat digabungkan dengan bangun datar lainnya. Kemudian gabungan dari bangun datra tersebut dapat ditentukan luas atau keliling sesuai dengan panjang dan lebar dari bangun-bangun tersebut.
Artikel di bawah ini berisikan mengenai 20 latihan soal yang berhubungan dengan luas dan keliling gabungan bangun datar. Adapun contoh soalnya seperti di bawah ini.

SOAL
Perhatikan gambar di bawah ini!

1. Berapa keliling gabungan bangun datar di atas?
- 50 cm
- 60 cm
- 70 cm
- 80 cm
Untuk menjawab soal no 2-5 perhatikan gambar di bawah ini

2. Gabungan bangun datar di atas membentuk bangun datar … dan …
- Persegi dan segitiga
- Persegi panjang dan trapesium
- Persegi panjang dan segitiga
- Belah ketupat dan jajar genjang
3. Berapa keliling persegi panjang di gambar tersebut?
- 64 cm
- 46 cm
- 72 cm
- 27 cm
4. Gabungan kedua bangun datar tersebut mmebntuk bangun datar baru, yaitu …
- Jajar genjang
- Belah ketupat
- Layang-layang
- Trapesium
5. Luas gabungan bangun datar tersebut adalah …
- 300 cm²
- 600 cm²
- 900 cm²
- 1.200 cm²
6. Perhatikan gambar berikut ini!

Berapa luas bangun datar di atas jika diketahui tinggi segitiga adalah 4 cm …
- 40 cm²
- 80 cm²
- 120 cm²
- 160 cm²
7. ½ x d1 x d2 merupakan rumus yang digunakan untuk mencari … layang-layang
- Panjang sisi
- Diagonal
- Luas
- Keliling
Perhatikan gambar di bawah ini!

Keliling bangun datar di atas adalah …
- 211 cm²
- 121 cm²
- 212 cm²
- 112 cm²
Untuk menjawab soal no 9 dan 10 perhatikan gambar di bawah ini!
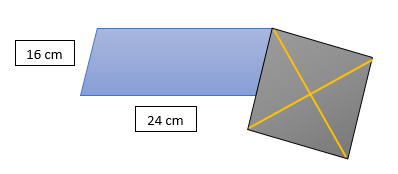
Diketahui masing-masing diagonal belah ketupat adalah 12 cm dan 14 cm.
9. Berapa luas belah ketupat tersebut?
- 168 cm²
- 84 cm²
- 72 cm²
- 36 cm²
10. Berapa keliling jajar genjang di atas?
- 80 cm
- 48 cm
- 32 cm
- 50 cm
11. Rumus untuk mencari luas jajar genjang adalah …
- p x l
- b. ½ x a x t
- c. a x t
- d. ½ x d1 x d2
Perhatikan gambar di bawah ini!

Diketahui dua buah trapesium dengan atas 12 cm, bawah, 16 cm, dan tinggi 10 cm.
12. Berapa luas kedua trapesium di atas?
- 45 cm²
- 75 cm²
- 90 cm²
- 180 cm²
Untuk menjawab soal no 13-15 perhatikan gambar berikut ini!

Tinggi segitiga pada gabungan bangun datar tersebut adalah 6 cm.
13. Nama bangun datar yang diarsir adalah …
- Persegi
- Persegi panjang
- Segitiga
- Trapesium
14. Luas bangun datar yang tidak diarsir adalah …
- 363 cm²
- 336 cm²
- 633 cm²
- 636 cm²
15. Berapa luas gabungan bangun datar di atas?
- 405 cm²
- 406 cm²
- 407 cm²
- 408 cm²
Perhatikan gambar di bawah ini!

16. Berapa luas daerah yang tidak diarsir jika diketahui tinggi segitiga adalah 16 cm …
- 468 cm²
- 278 cm²
- 668 cm²
- 787 cm²
Perhatikan gambar di bawah ini!

17. Berapa luas daerah yang tidak diarsir?
- 24 cm²
- 42 cm²
- 32 cm²
- 23 cm²
Untuk menjawab soal no 18-20 perhatikan gambar berikut ini!

18. Disebut apakah segitiga pada gambar di atas?
- Segitiga sama sisi
- Segitiga sama kaki
- Segitiga siku-siku
- Segitiga sembarang
19. Berapa luas segitiga kecil?
- 15 cm²
- 30 cm²
- 45 cm²
- 60 cm²
20. Berapa luas keseluruhan bangun datar di atas?
- 151 cm²
- 153 cm²
- 154 cm²
- 156 cm²
Jawaban dan Pembahasan
1. B. 60 cm
15 cm + 7 cm + 10 cm + (15-7) + 5 + 15 = 60 cm
2. C. Persegi panjang dan segitiga
Kedua bangun datar yang tertera dalam gambar adalah persegi panjang dan segitiga
3. A. 64 cm
Keliling persegi panjang
= 2 (p+l)
= 2 (20 + 12)
= 2 x 32
= 64 cm
4. D. Trapesium
Gabungan kedua bangun datar tersebut membentuk trapesium
5. A. 300 cm²
Luas persegi panjang
= p x l
= 20 x 12
= 240 cm²
Luas segitiga
= ½ x a x t
= ½ x 10 x 12
= ½ x 120
= 60 cm²
Total luas keseluruhan
= luas persegi panjang + luas segitiga
= 240 + 60
= 300 cm²
6. B. 80 cm²
Luas persegi
= s x s
= 8 x 8
= 64 cm²
Luas segitiga
= ½ x a x t
= ½ x 8 x 4
= ½ x 32
= 16 cm²
Luas total gabungan bangun datar
= luas persegi + luas segitiga
= 64 + 16
= 80 cm²
7. C. Luas
½ x d1 x d2 merupakan rumus untuk mencari luas layang-layang
8. D. 112 cm²
Keliling persegi panjang
= 2 x (p + l)
= 2 x (24 + 14)
= 2 x 38
= 76 cm²
Keliling setengah lingkaran
Diameter = 14 cm
Jari-jari (r) = ½ x 14 = 7 cm
= πr + 2r
= 22/7 x 7 + (2 x 7)
= 22 + 14
= 36 cm²
Jadi, keliling bangun datar
Keliling persegi panjang + keliling setengah lingkaran
= 76 + 36
= 112 cm²
9. B. 84 cm²
Luas belah ketupat
= ½ x d1 x d2
= ½ x 12 x 14
= ½ x 168
= 84 cm²
10. A. 80 cm
Keliling jajar genjang
= 2 x (a + b)
= 2 x (24 + 16)
= 2 x 40
= 80 cm
11. C. a x t
Rumus untuk mencari luas jajar genjang adalah a x t
12. D. 180 cm²
Luas trapesium
= ½ x (a + b) x t
= ½ x (12 + 16) x 10
= ½ x 18 x 10
= ½ x 180
= 90 cm²
Karena kedua trapesium memiliki ukuran yang sama, maka
2 x 90
= 180 cm²
13. C. Segitiga
Nama bangun datar yang diarsir adalah segitiga
14. B. 336 cm²
Bangun datar yang tidak diarsir adalah persegi panjang
Luas persegi panjang
= p x l
= 28 x 12
= 336 cm²
15. D. 408 cm²
Gabungan bangun datar tersebut terdiri dari 1 persegi panjang dan 2 segitiga, maka
Luas persegi panjang
= p x l
= 28 x 12
= 336 cm²
Luas segitiga
= ½ x a x t
= ½ x 12 x 6
= ½ x 72
= 36 cm²
Terdapat 2 segitiga, maka 2 x 36 = 72 cm²
Luas total gabungan bangun datar tersebut adalah
Luas persegi panjang + luas 2 segitiga
= 336 + 72
= 408 cm²
16. A. 468 cm²
Luas persegi
= s x s
= 676 cm²
Luas segitiga
= ½ x a x t
= ½ x 26 x 16
= ½ x 416
= 208 cm²
Luas daerah yang tidak diarsir
Luas persegi – luas segitiga
= 676 – 208
= 468 cm²
17. B. 42 cm²
Luas persegi
= s x s
= 14 x 14
= 196 cm²
Luas lingkaran
Diameter = 14 cm
Jari-jari (r) = ½ x d = ½ x 14 = 7 cm
= π x r²
= 22/7 x 7 x 7
= 154 cm²
Luas bangun datar yang tidak diarsir adalah
Luas persegi – luas lingkaran
= 196 – 154
= 42 cm²
18. C. Segitiga siku-siku
Jawaban yang tepat adalah C
19. B. 30 cm²
Luas segitiga kecil
= ½ x a x t
= ½ x 10 x (20-14)
= ½ x 10 x 6
= ½ x 60
= 30 cm²
20. D. 156 cm²
Luas segitiga kecil
= ½ x a x t
= ½ x 10 x (20-14)
= ½ x 10 x 6
= ½ x 60
= 30 cm²
Luas segitiga besar
= ½ x a x t
= ½ x 18 x 14
= ½ x 252
= 126 cm²
Luas keseluruhan bangun datar tersebut adalah
Luas segitiga kecil + luas segitiga besar
= 30 + 126
= 156 cm²